Skip to main content

Compute results with cardinality sketches

Analyzing large datasets to produce exact counts consumes considerable compute resources. Operations that don't require exact counts and can tolerate a certain error rate may benefit from a class of specialized approximation algorithms, called cardinality sketches.

Cardinality sketches are approximate, mergeable, and limited-size representations of potentially large amounts of input data that trade off accuracy for reduced storage and improved performance. Cardinality sketches use various randomization techniques to produce approximate aggregates of data and deliver results with mathematically proven error bounds. Using cardinality sketches at ingestion and query time can significantly reduce processing costs and improve query performance.

This topic provides an overview of cardinality sketches supported by Imply Polaris. All examples are based on the sample Wikipedia dataset.

Types of cardinality sketches​

Polaris uses the Apache DataSketches library of stochastic streaming algorithms to implement sketch modules. The DataSketches library includes various types of sketches, each one designed to solve a different sort of problem. Polaris supports HyperLogLog (HLL) and Theta cardinality sketches.

HyperLogLog​

The HyperLogLog (HLL) sketch aggregator is a very compact sketch algorithm for approximate distinct counting. During ingestion, the HLL aggregator creates HLL sketch objects. At query time, Polaris reads and merges the HLL sketch objects together returning approximate count of distinct values. You can also use the HLL aggregator to calculate a union of HLL sketches. For more information on HLL sketches, see DataSketches HLL Sketch module and Druid SQL HLL sketch functions.

Theta​

The Theta sketch is a sketch algorithm for approximate distinct counting with set operations. Theta sketches let you count the overlap between sets, so that you can compute the union, intersection, or set difference between sketch objects. During ingestion, the Theta aggregator creates Theta sketch objects. At query time, Polaris reads and merges the Theta sketch objects together returning approximate count of unique entries. For more information on Theta sketches, see DataSketches Theta Sketch module and Druid SQL Theta sketch functions.

Choosing a sketch type​

HLL and Theta sketches both support approximate distinct counting; however, the HLL sketch produces more accurate results and consumes less storage space. Theta sketches are more flexible but require significantly more memory.

When choosing an approximation algorithm for your use case, consider the following:

  • If your use case entails distinct counting and merging sketch objects, use the HLL sketch.
  • If you need to evaluate union, intersection, or difference set operations, use the Theta sketch.

You cannot merge HLL sketches with Theta sketches.

Ingest sketches​

To ingest data as sketch objects, follow these steps:

  1. Create an aggregate table. The Polaris table schema only accepts sketch columns as measures.
  2. On the Map source to table page, where you map input fields to table columns, click the plus icon to add a new measure.
  3. In the Measure dialog dialog, enter the column information:
    • Name: The column name.
    • Data type: Choose between Theta sketch or HLL sketch data types.
    • Input expression: The sketch aggregation function. You can tune the size and accuracy of a sketch through the optional parameters passed into the sketch aggregator.
      • For HLL sketches, use the HLL aggregator DS_HLL(expr, [lgK, tgtHllType])—for example, DS_HLL("inputField").
      • For Theta sketches, use the Theta aggregator DS_THETA(expr, [size])—for example, DS_THETA("inputField").

The following screenshot shows the Sketches-demo aggregate table with the HLL sketch HLL_user column after ingestion. Note that Polaris displays sketches as Base64-encoded strings.

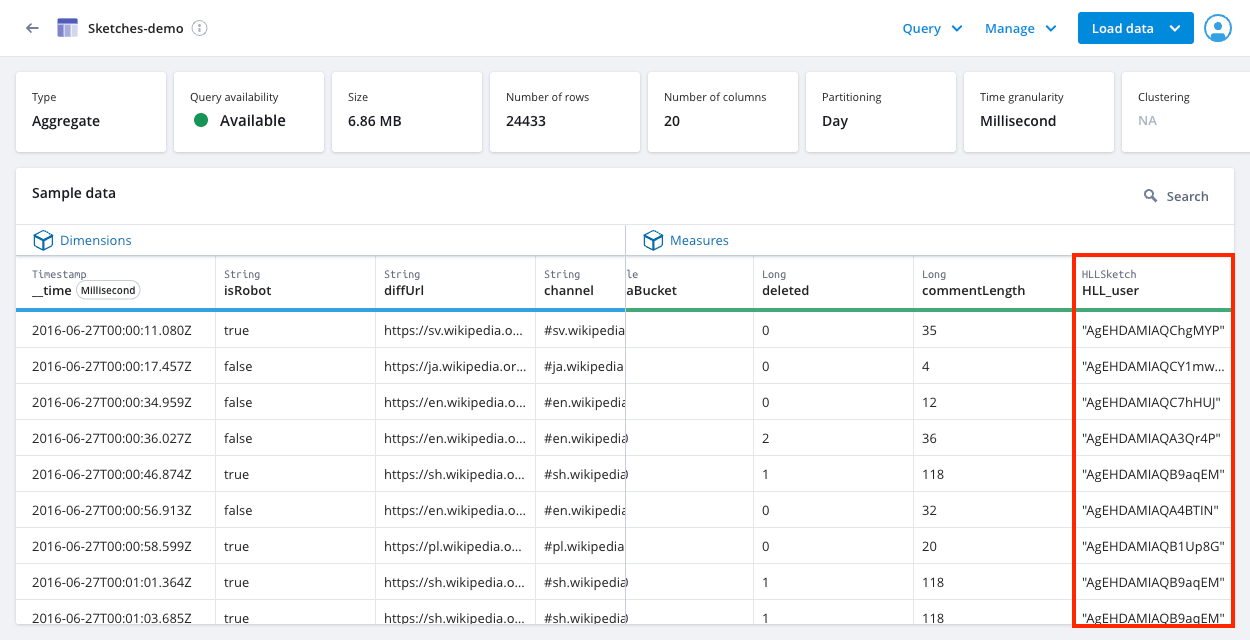
Sketches HLLSketch data type

Ingest pre-computed data sketches​

Polaris can ingest pre-computed sketches that are stored as Base64-encoded strings. Make sure that the data type of the input field that maps to the sketch column is string. At ingestion time, use the appropriate sketch aggregation function with DECODE_BASE64_COMPLEX to convert the Base64-encoded strings to sketch objects in Polaris.

FunctionDescription
DECODE_BASE64_COMPLEX(dataType, expr)Decodes a Base64-encoded string into a complex data type, such as thetaSketch or HLLSketch, where dataType represents the complex type and expr is the Base64-encoded string to decode.

The following examples how to ingest pre-computed cardinality sketches:

  • Ingest pre-computed Theta sketches: DS_THETA(DECODE_BASE64_COMPLEX('thetaSketch', "theta_input"))
  • Ingest pre-computed HLL sketches: DS_HLL(DECODE_BASE64_COMPLEX('HLLSketch', "hll_input"))

To use this function with Quantiles sketches, see Create a Quantiles sketch.

Query sketched data​

To use sketches during query in the Polaris UI, do the following:

  1. On the Table detail page, click Query in the top-right corner.

  2. Select SQL console.

    The following screenshot shows the Query dropdown menu:

    Query dropdown

  3. Enter your query in the SQL query tab.

  4. Click Run.

Sample queries​

These examples are based on the sample Wikipedia dataset.

The following sample query uses the APPROX_COUNT_DISTINCT_DS_HLL aggregation function to count distinct values of a regular column named user:

SELECT APPROX_COUNT_DISTINCT_DS_HLL(user) AS unique_users
FROM "Sketches-demo"
WHERE isRobot = 'false'

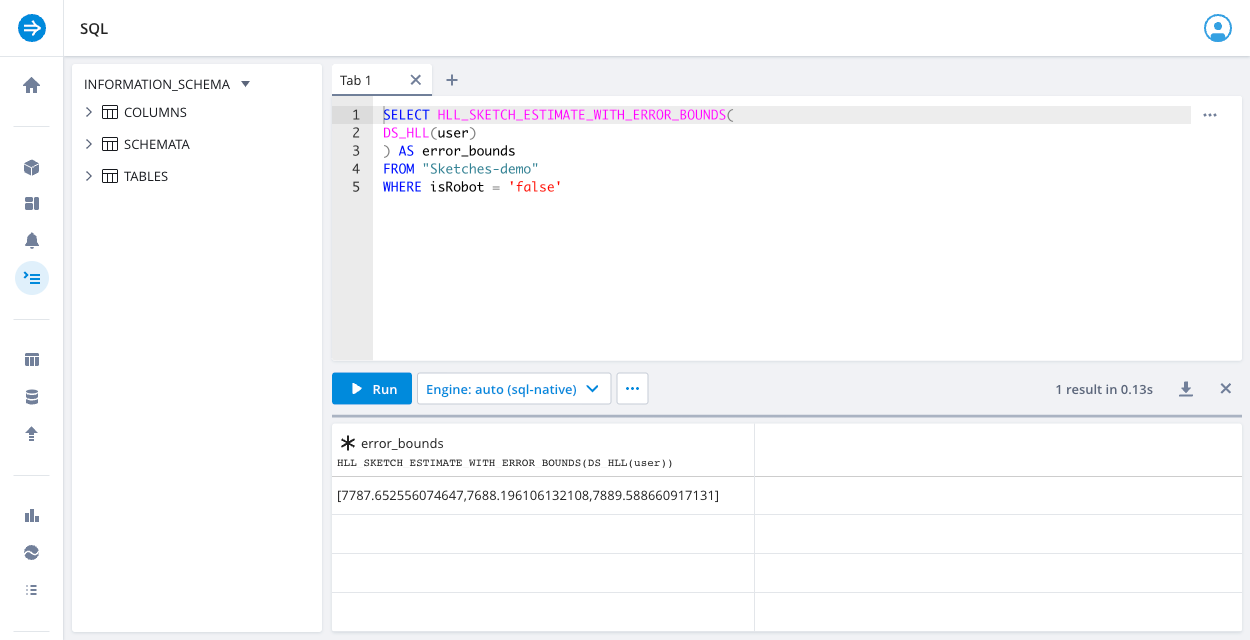
The following sample query uses the HLL_SKETCH_ESTIMATE_WITH_ERROR_BOUNDS function to return the distinct count estimate with error bounds:

SELECT HLL_SKETCH_ESTIMATE_WITH_ERROR_BOUNDS(
  DS_HLL(user)
) AS error_bounds
FROM "Sketches-demo"
WHERE isRobot = 'false'

HLL query example

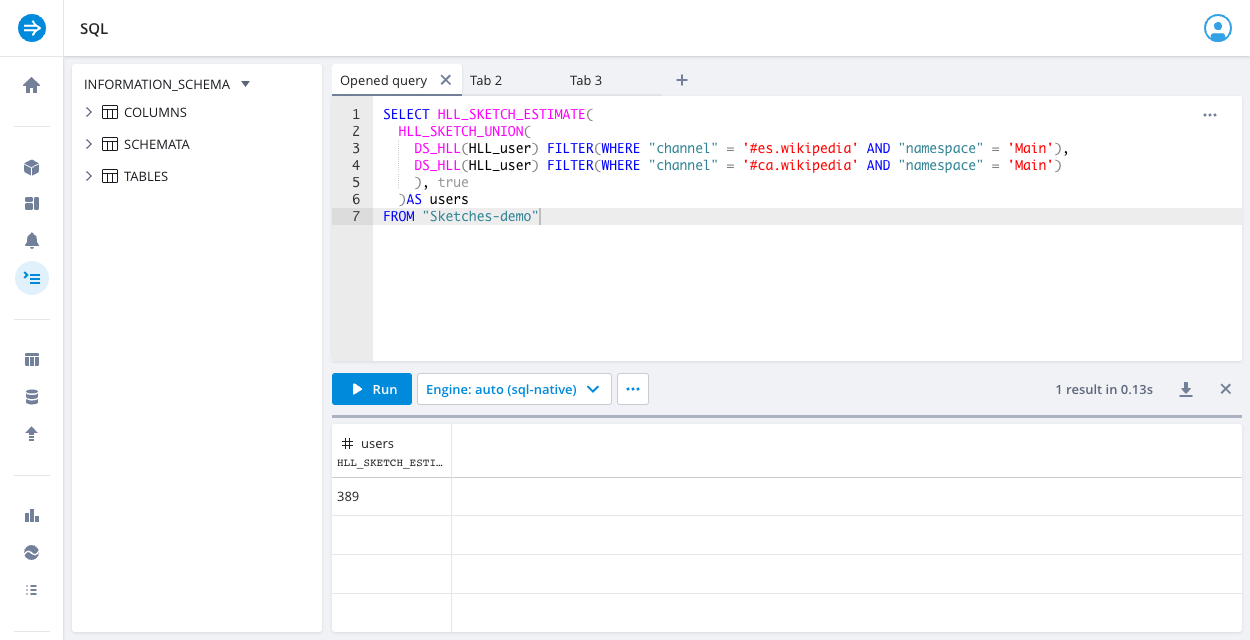
The following sample query uses the HLL_SKETCH_UNION function to calculate the number of users who visited pages in the main namespace of the Spanish and Catalan editions of Wikipedia:

SELECT HLL_SKETCH_ESTIMATE(
  HLL_SKETCH_UNION(
    DS_HLL(user) FILTER(WHERE "channel" = '#en.wikipedia' AND "namespace" = 'Main'),
    DS_HLL(user) FILTER(WHERE "channel" = '#ca.wikipedia' AND "namespace" = 'Main')
) AS users
FROM "Sketches-demo"

HLL union query example

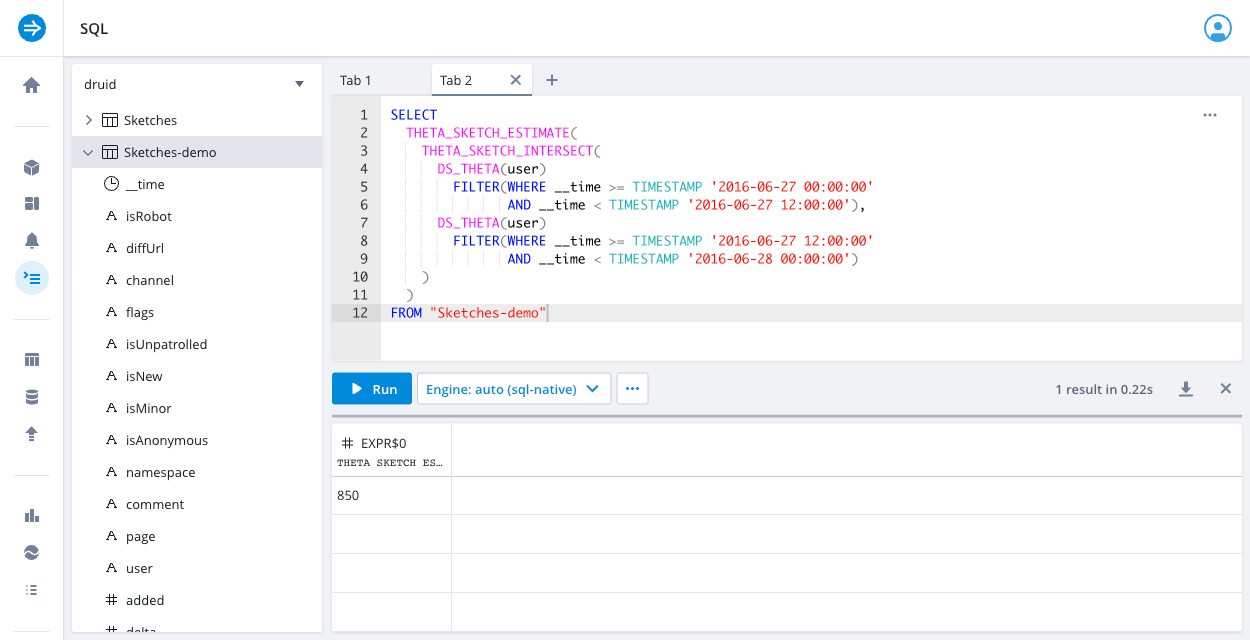
The following sample query examines how many users from one time period, 2016-06-27 00:00:00 to 2016-06-27 12:00:00, also appear in another time period, 2016-06-27 12:00:00 to 2016-06-28 00:00:00:

SELECT 
  THETA_SKETCH_ESTIMATE(
    THETA_SKETCH_INTERSECT(
      DS_THETA(user)
        FILTER(WHERE __time >= TIMESTAMP '2016-06-27 00:00:00'
               AND __time < TIMESTAMP '2016-06-27 12:00:00'),
      DS_THETA(user)
        FILTER(WHERE __time >= TIMESTAMP '2016-06-27 12:00:00'
               AND __time < TIMESTAMP '2016-06-28 00:00:00')
    )
  )
FROM "Sketches-demo"

Theta query example

Relative error of sketches​

Sketches are stochastic processes and the estimates produced are random variables that follow a normal distribution given the central limit theorem. For scenarios in which the error distribution is not normally distributed, see The Error Distribution is Not Gaussian.

Because sketches are probabilistic, they don't have a "maximum error." Sketch accuracy is usually measured in terms of relative error or expected error.

You can calculate error bounds for distinct count estimates on sketches using the following sketch scalar functions:

  • HLL_SKETCH_ESTIMATE_WITH_ERROR_BOUNDS(sketchColumn, numStdDev)
  • THETA_SKETCH_ESTIMATE_WITH_ERROR_BOUNDS(sketchColumn, numStdDev)

Each function takes a parameter for the number of standard deviations, which determines the confidence intervals. Choose the number of standard deviations based on the desired relative error. You can use relative error at the 99.73% confidence level as a reference benchmark; most of the time your error will be less than this value.

HLL sketch relative error​

For HLL sketches created in Polaris using the default size and accuracy parameters, the relationship applies for the number of standard deviations, confidence intervals, and relative error:

Number of standard deviationsConfidence intervalsHLL relative error
168.27%1.63%
295.45%3.25%
399.73%4.88%

If you query the sketch column with 3 standard deviations for the 99.73% confidence interval, the average relative error of the distinct count result is within 4.88% of the true value.

Theta sketch relative error​

For Theta sketches created in Polaris using the default size and accuracy parameters, the relationship applies for the number of standard deviations, confidence intervals, and relative error:

Number of standard deviationsConfidence intervalsTheta relative error
168.27%0.78%
295.45%1.56%
399.73%2.34%

Comparing sketch relative error​

While the relative errors for Theta sketches appear lower than HLL sketches, these reflect differences in the default parameters that control size and accuracy when creating sketches. The following values describe the default tuning parameters when creating sketches:

  • For HLL sketches, lgK is 12.
  • For Theta sketches, size is 16,384.

The analogous log base 2 value for Theta sketches is log2(16384) = 14, which is greater than 12. For equivalent log base 2 of size values, both sketches have similar accuracy although Theta sketches take thirty times more memory and is slower than HLL sketches.

When deciding what sketch type to use, do not use accuracy as the deciding factor. Prioritize your query use cases; you can increase the sketch size for more accurate estimates.

For more details on relative error of sketches, see the following resources:

Learn more​

See the following topics for more information: